U.2. DIVISIBILIDAD

 

ÍNDICE:

1. Múltiplos de un número.

2. Divisores de un número.

3. Criterios de divisibilidad.

4. Cálculo de todos los divisores de un número.

5. Números primos y compuestos.

6. Mínimo común múltiplo. (m.c.m.)

7. Máximo común divisor. (M.c.d.)

8. Problemas de m.c.m y M.c.d.

1 y 2 Múltiplos y divisores de un número. 

Diferencias entre múltiplo y divisor de un número.

  Los múltiplos de un número son los resultados de multiplicar ese número por cualquier número natural.
  M (7)={0, 7, 14, 21, 28, 35, 42, ...}
  Decimos que un número es múltiplo de otro si lo contiene un número entero de veces.

 Los divisores de un número son aquellos que pueden dividir a un número y su división es exacta.
    • Todos los números naturales son divisores de 0.
    • El número 1 tiene un solo divisor, es el 1.
       D(18)={1, 2, 3, 6, 9, 18}

3. Criterios de divisibilidad.

    Para calcular los divisores de un número tenemos que tener en cuenta los criterios de divisibilidad para calcular algunos divisores más rápido.

Aquí tenéis a nuestros amigos Troncho y Poncho para animaros.

4. Cálculo de todos los divisores de un número.

    Los divisores de un número natural son los números naturales que lo pueden dividir, resultando de cociente y divisor otro número natural y de resto 0.

    La manera más sencilla de calcular los divisores de un número es realizando las divisiones de ese número entre los números naturales, hasta que el el cociente sea igual o menor al divisor.

Ejemplo: Calcula todos los divisores de 12.

12 : 1= 12.  Esto significa 1 y 12 son divisores de 12.

12 : 2= 6. Esto significa 2 y 6 son divisores de 12.

12 : 3= 4. Entonces también 3 y 4 son divisores de 12.

12:  4 = 3.  Ahora podemos parar porque ya hemos encontrado un cociente menor que el divisor. No habrá más divisores. 

Entonces el conjunto de divisores de 12 son D(12)={1,2,3,4,6,12}.

5. Números primos y compuestos. 

Al comprobar cuántos divisores tienen los números observamos que:

Los números primos son los que tienen dos divisores, que son el 1 y el mismo número primo.
Los números compuestos son los que tienen más de dos divisores, son los más frecuentes.

Descomposición factorial en factores de números primos.

La descomposición factorial o factorización de un número en factores primos, consiste en expresar un número como la multiplicación de sus factores primos de la siguiente forma:

La forma más usada consiste en ir dividiendo el número entre los divisores primos: 2,3,5,7,11,13..., hasta que solo quede el número 1.

Por ejemplo: 

Realiza la descomposición en producto de factores primos del número 24:

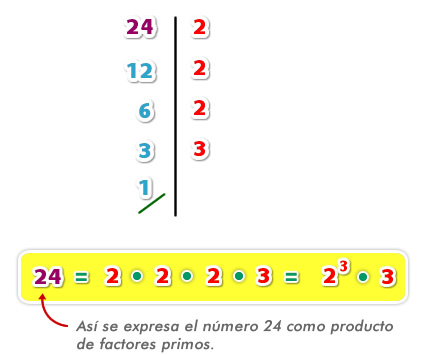
1° Se escribe el número a la izquierda de una raya vertical  y a su derecha el menor número primo (2, 3, 5, 7,... ) por el cual dicho número sea divisible. El cociente obtenido se coloca debajo del número propuesto. 

2° Se procede como en el paso anterior con el cociente obtenido, y así sucesivamente hasta llegar a un cociente igual a 1.

¿Para qué se utiliza la descomposición factorial?

La utilizamos para:

• Calcular el máximo común divisor de dos o más números los descomponemos en su producto de factores primos y cogemos de los factores comunes el de menor exponente.

                Ejemplo: 

                M.c.d. (12,50)= 2

                 12= 2² x 3          

                 50= 2 x 5²        2² > 2

    

• Calcular el mínimo común múltiplo de dos o más números los descomponemos en su producto de factores primos y cogemos de los factores comunes el de mayor exponente y todos los no comunes.

                Ejemplo:

                m.c.m. (12,50)= 2² x 3 x 5² = 300

                12= 2² x 3          

                 50= 2 x 5²        2² > 2 

6. Mínimo común múltiplo (m.c.m).

Dados dos o más números podemos calcular múltiplos de cada uno y observaremos como hay números que son múltiplos a la vez de todos ellos.

De estos múltiplos comunes vamos a considerar el más pequeño, sin contar el 0, a ese lo llamaremos el mínimo común múltiplo y lo indicaremos abreviadamente m.c.m.

7. Máximo común divisor (M.c.d.)

Dados dos o más números podemos calcular los divisores de cada uno y observar si hay algunos que sean divisores a la vez de todos ellos.

De estos divisores comunes vamos a considerar el más grande, a ese lo llamaremos el máximo común divisor y lo indicaremos abreviadamente M.c.d.

Cuando resulta que el único divisor común de dos números es el 1, se dicen primos entre sí.


            Por ejemplo 14 y 15,
                 • divisores de 14: 1, 2, 7, 14
                 • divisores de 15: 1, 3, 5, 15

8. Problemas de m.c.m. y M.c.d.

Lo difícil de estos problemas es saber cual de los dos contenidos debemos utilizar pero,... tranquilos que los problemas nos ayudan, dando pistas, 😎

• Alan y Pedro comen en la misma taquería, pero Alan asiste cada 20 días y Pedro cada 38. ¿Cuándo volverán a encontrarse? ¿¿mcm o Mcd??😕

• Andrés tiene una cuerda de 120 metros y otra de 96 metros. Desea cortarlas de modo que todos los trozos sean iguales pero lo más largos posible. ¿Cuántos trozos de cuerda obtendrá? ¿¿mcm o Mcd??😕

• En una calle se están instalando dos semáforos: uno de ellos se pondrá en verde cada 3 minutos y el otro, cada 5 minutos. Una vez se conectan los semáforos, ¿cuánto tiempo tardarán en ponerse en verde al mismo tiempo por primera vez? ¿¿mcm o Mcd??😕

•  Una habitación tiene 230cm de largo por 120cm de largo. Queremos cubrir el suelo con baldosas cuadradas. ¿Cuánto tienen que medir estas baldosas? ¿Cuántas baldosas harán falta? ¿¿mcm o Mcd??😕

Planteamiento: debemos calcular el M.c.d de las dos medidas 

Operación: M.c.d (230 y 120)= 10

Solución: las baldosas tendrán que tener 10 centímetros de lado.

Un largo de 230cm necesitaría 23 baldosas; un ancho de 120cm, necesitaría 12 baldosas. Por lo tanto, harían falta 23x12 = 276 baldosas.